homework_2 (Sensitivity, Specificity and Precision)

Let patient be positive for Nonmelanoma Skin Cancer, and healthy be negative for Nonmelanoma Skin Cancer. To evaluate the performance of a test or model, various measures, such as sensitivity, specificity, precision, recall,and area under the receiver operating characteristic curve (AUROC), are used. Classify patient or healthy produces four outcomes: True positive(TP) = the number of cases correctly identified as patient; False positive(FP) = the number of cases incorrectly identified as patient; True negative (TN) = the number of cases correctly identified as healthy; False negative (FN) = the number of cases incorrectly identified as healthy.

The sensitivity of a predicated model is its ability to predict the patient cases correctly. To estimate it, we should calculate the proportion of true positive in patient cases. Mathematically, this can be stated as:

\[Sensitivity = \frac{TP}{TP+FN}\]

The specificity of a test is its ability to predict the healthy cases correctly. To estimate it, we should calculate the proportion of true negative in healthy cases. Mathematically, this can be stated as:

\[Specificity = \frac{TN}{TN+FP}\]

Positive predictive value (PPV, also called precision) is the probability that subjects with a positive prediction truly have the disease. Mathematically, this can be stated as:

\[Precision = \frac{TP}{TP+FP}\]

Also, if the prevalence is known, this can be state as:

\(Sensitivity * Prevalence / [(Sensitivity * Prevalence) +\) \(((1- Specificity) * (1-Prevalence))]\)

Therefore, if a test has sensitivity = 80% and specificity 80% and the prevalence of the disease is 9/100,000, the PPV is

\[0.8 * 9/100000 / [(0.8 * 9/100000) + ((1- 0.8) * (1-9/100000))] \approx 0.00036\]

Suppose sensitivity = specificity, and the prevalence of the disease is 9/100,000, the figure between sensitivity/specificity and the PPV will be as follow:

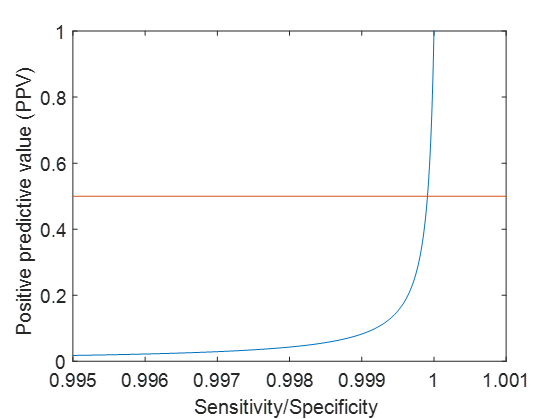
From the plot, we could see the sensitivity and specificity should be greater than 0.999 ($\approx 1$), if we want to achieve positive predictive value = 50%.

Table 2 of Wang et al. [1] showed the performances of convolutional neural network (CNN) with different input features. The CNN prediction model with both ICD-9-CM and drug prescriptions (model 3) as input features achieved an AUROC of 0.894 (0.007), sensitivity of 83.1%, specificity of 82.3% and precision of 0.571. It means the chance that a person with a positive prediction truly has the disease is 57.1%. PPV is influenced by the prevalence of disease in the population that is being tested. From the formula above, if the both the sensitivity and specificity are around 0.8, the precision is also very low when the prevalence is very low. Therefore, the generalizability of this model might be problematic and we need continue to optimize the model, increase the amount of data or validate the model against another database.

References

[1] Wang, Hsiao-Han, Yu-Hsiang Wang, Chia-Wei Liang, and Yu-Chuan Li. 2019. “Assessment of Deep Learning Using Nonimaging Information and Sequential Medical Records to Develop a Prediction Model for Nonmelanoma Skin Cancer.” Jama Dermatology 155 (11): 1277–83.